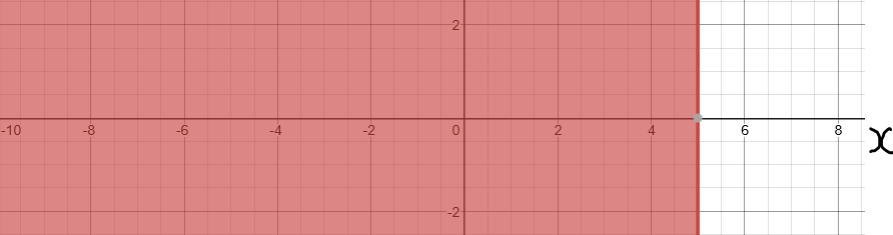
Solved Examples on Linear Inequalities

Pre-requisites: Expressions and Equations

For ACT Students
The ACT is a timed exam...$60$ questions for $60$ minutes
This implies that you have to solve each question in one minute.
Some questions will typically take less than a minute a solve.
Some questions will typically take more than a minute to solve.
The goal is to maximize your time. You use the time saved on those questions you solved in less than a minute, to solve the questions that will take more than a minute.
So, you should try to solve each question correctly and timely.
So, it is not just solving a question correctly, but solving it correctly on time.
Please ensure you attempt all ACT questions.
There is no negative penalty for any wrong answer.

For JAMB and CMAT Students
Calculators are not allowed. So, the questions are solved in a way that does not require a calculator.

Unless specified otherwise:
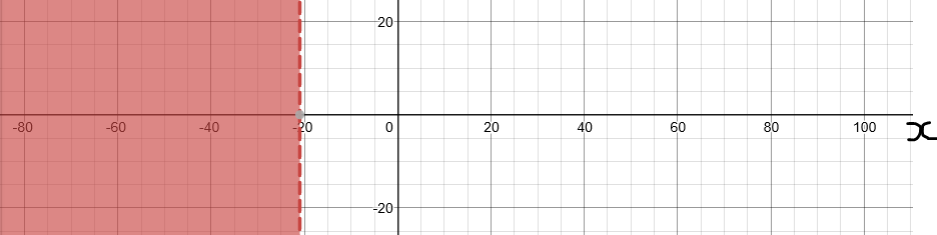
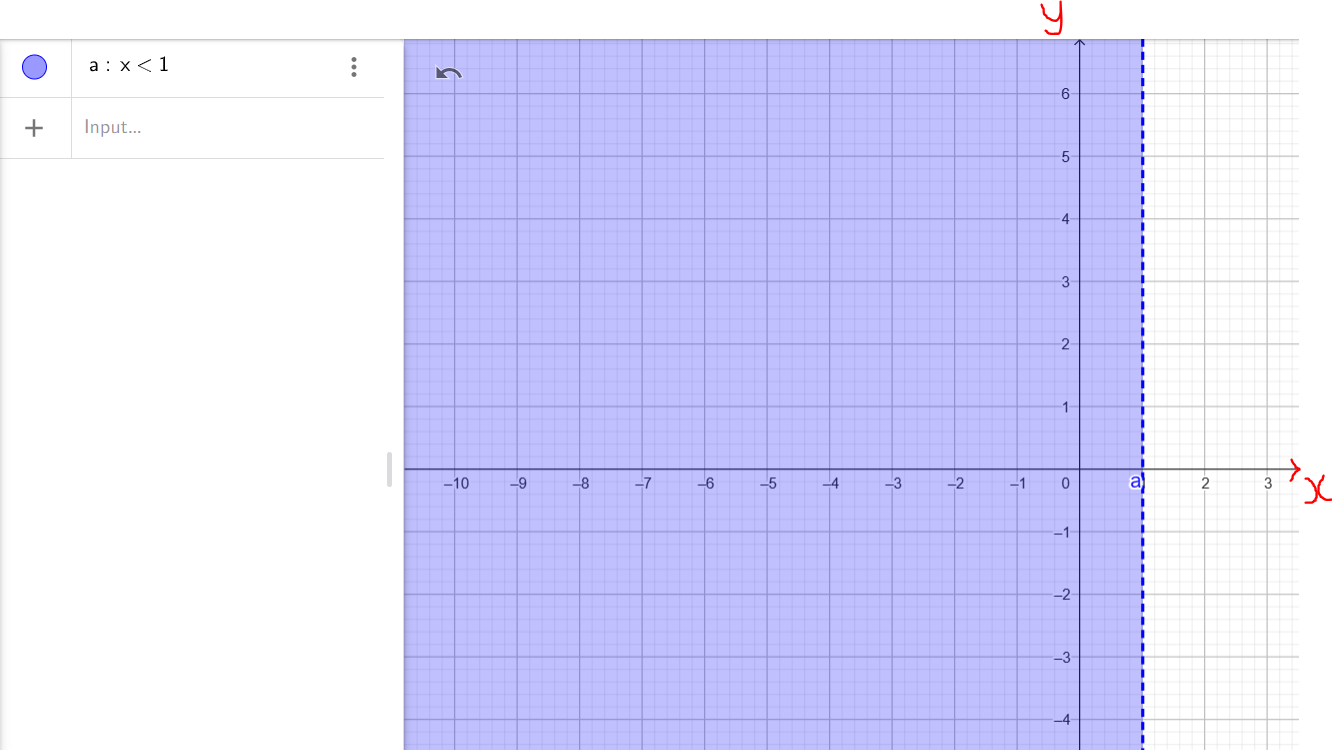
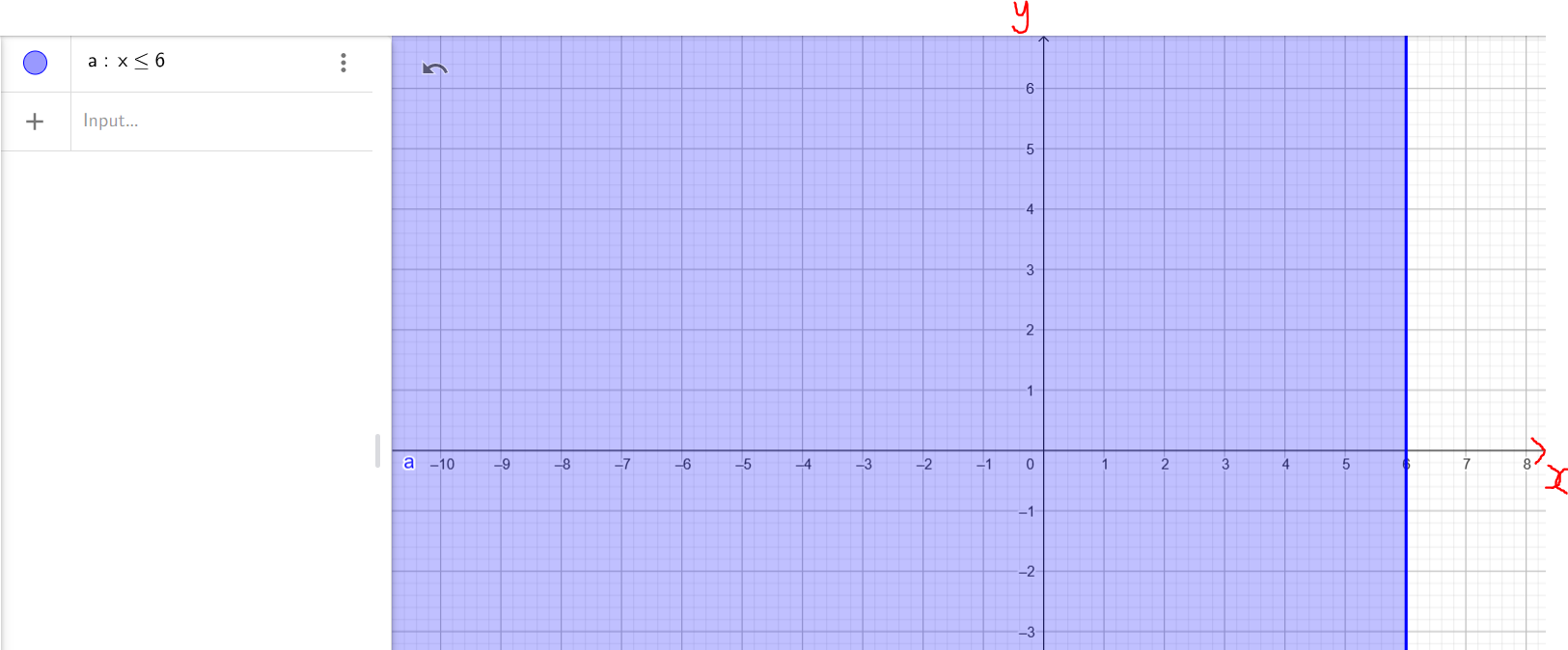
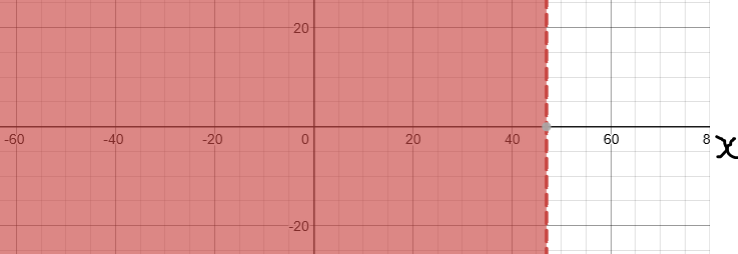
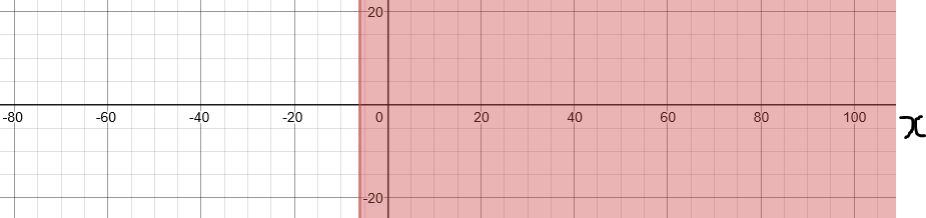
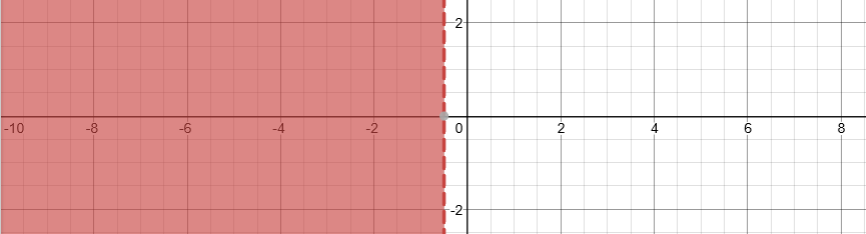
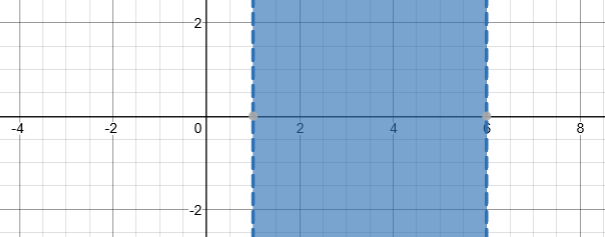
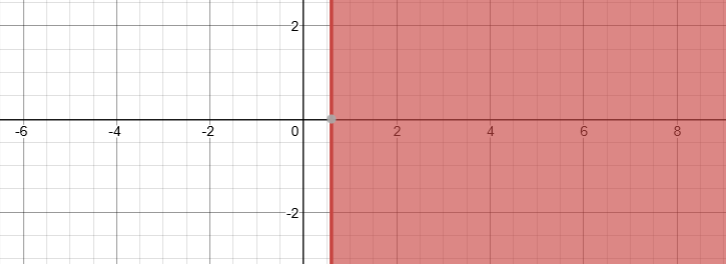
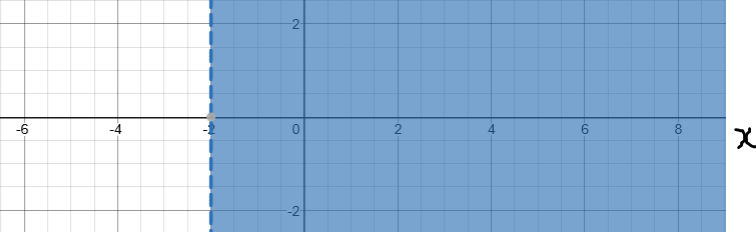
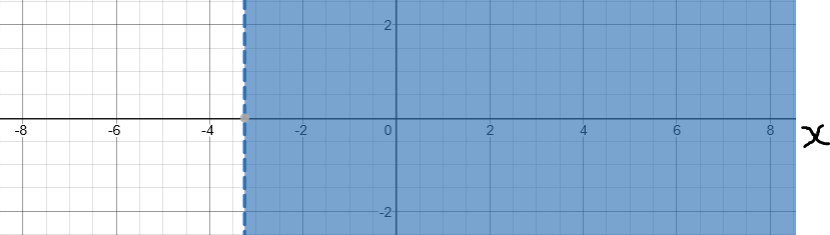
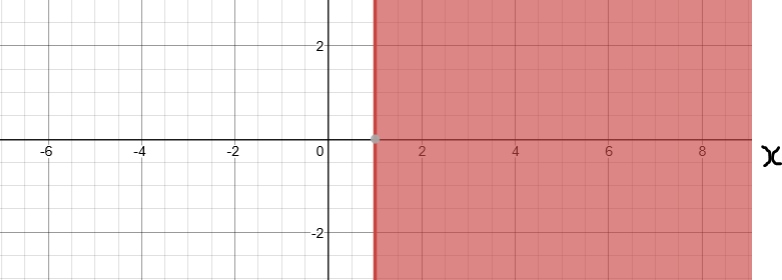
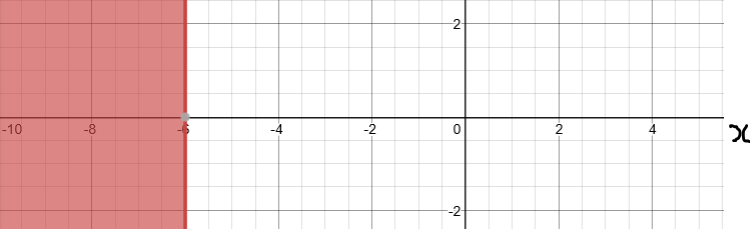
Solve, Check, and Graph these inequalities.
Write each solution in set notation.
Write each solution in interval notation.

(1.) $x + 18 \lt -3$

$ x + 18 \lt -3 \\[3ex] x \lt -3 - 18 \\[3ex] x \lt -21 \\[3ex] Set\:\:Notation:\:\: \{x | x \lt -21\} \\[3ex] Interval\:\:Notation:\:\:(-\infty, -21) \\[3ex] $

Check

$ \underline{LHS} \\[3ex] x + 18 \\[3ex] x \lt -21 \\[3ex] Let\:\: x = -25 \\[3ex] -25 + 18 \\[3ex] -25 + 18 \\[3ex] -7 $	$ \underline{RHS} \\[3ex] -3 $
$-7 \lt -3$

(2.)
(a.) 3x + 5 < 8
(b.) −2x − 4 ≤ 8 − 4x

$ (a.) \\[3ex] 3x + 5 \lt 8 \\[3ex] 3x \lt 8 - 5 \\[3ex] 3x \lt 3 \\[3ex] x \lt \dfrac{3}{3} \\[5ex] x \lt 1 \\[3ex] Set\:\:Notation:\:\: \{x | x \lt 1\} \\[3ex] Interval\:\:Notation:\:\:(-\infty, 1) \\[3ex] $

Check

$ \{x | x \lt 1\} \\[3ex] Let\;\;x = 0 $
LHS	RHS
$ 3x + 5 \\[3ex] 3(0) + 5 \\[3ex] 0 + 5 \\[3ex] 5 $	$8$
$5 \lt 8$

$ (b.) \\[3ex] -2x - 4 \le 8 - 4x \\[3ex] -2x + 4x \le 8 + 4 \\[3ex] 2x \le 12 \\[3ex] x \le \dfrac{12}{2} \\[5ex] x \le 6 \\[3ex] Set\:\:Notation:\:\: \{x | x \le 6\} \\[3ex] Interval\:\:Notation:\:\:(-\infty, 6] \\[3ex] $

Check

$ \{x | x \le 6\} \\[3ex] Let\;\;x = 0 $
LHS	RHS
$ -2x - 4 \\[3ex] -2(0) - 4 \\[3ex] 0 - 4 \\[3ex] -4 $	$ 8 - 4x \\[3ex] 8 - 4(0) \\[3ex] 8 - 0 \\[3ex] 8 $
$-4 \le 8$

(3.) ACT The inequality $6(x + 2) \gt 7(x - 5)$ is equivalent to which of the following inequalities?

$ A.\:\: x \lt -23 \\[3ex] B.\:\: x \lt 7 \\[3ex] C.\:\: x \lt 17 \\[3ex] D.\:\: x \lt 37 \\[3ex] E.\:\: x \lt 47 \\[3ex] $

$ 6(x + 2) \gt 7(x - 5) \\[3ex] Distributive\:\:Property \\[3ex] 6x + 12 \gt 7x - 35 \\[3ex] Swap.\:\:To\:\:avoid\:\:division\:\:by\:\:a\:\:negative\:\:number(my\:\:preference) \\[3ex] 7x - 35 \lt 6x + 12 \\[3ex] 7x - 6x \lt 12 + 35 \\[3ex] x \lt 47 \\[3ex] Set\:\:Notation:\:\: \{x | x \lt 47\} \\[3ex] Interval\:\:Notation:\:\:(-\infty, 47) \\[3ex] $

Check

$ \underline{LHS} \\[3ex] 6(x + 2) \\[5ex] x \lt 47 \\[3ex] Let\:\: x = 0 \\[3ex] 6(0 + 2) \\[3ex] = 6(2) \\[3ex] = 12 $	$ \underline{RHS} \\[3ex] 7(x - 5) \\[3ex] Must\:\: use\:\: x = 0 \\[3ex] = 7(0 - 5) \\[3ex] = 7(-5) \\[3ex] = -35 $
$12 \gt -35$

(4.) ACT The solution set of $2x + 4 \ge -8$ is the set of all real values of $x$ such that:

$ 2x + 4 \ge -8 \\[3ex] 2x \ge -8 - 4 \\[3ex] 2x \ge -12 \\[3ex] x \ge -\dfrac{12}{2} \\[5ex] x \ge -6 \\[3ex] Set\:\:Notation:\:\: \{x | x \ge -6\} \\[3ex] Interval\:\:Notation:\:\:[-6, \infty) \\[3ex] $

Check

$\{x | x \ge -6\}$
LHS	RHS
$ 2x + 4 \\[3ex] x \ge -6 \\[3ex] Let\:\: x = 0 \\[3ex] 2(0) + 4 \\[3ex] 0 + 4 \\[3ex] 4 $	$-8$
$4 \ge -8$

(5.) WASSCE Solve $7x + 4 \lt \dfrac{1}{2}(4x + 3)$ and illustrate your answer on a number line.

$ 7x + 4 \lt \dfrac{1}{2}(4x + 3) \\[5ex] LCD = 2 \\[3ex] 2(7x + 4) \lt 2 * \dfrac{1}{2}(4x + 3) \\[5ex] 14x + 8 \lt 1(4x + 3) \\[3ex] 14x + 8 \lt 4x + 3 \\[3ex] 14x - 4x \lt 3 - 8 \\[3ex] 10x \lt -5 \\[3ex] x \lt -\dfrac{5}{10} \\[5ex] x \lt -\dfrac{1}{2} \\[5ex] Set\:\:Notation:\:\: \left\{x | x \lt -\dfrac{1}{2}\right\} \\[5ex] Interval\:\:Notation:\:\:\left(-\infty, -\dfrac{1}{2}\right) \\[5ex] $

Check

$ \underline{LHS} \\[3ex] 7x + 4 \\[5ex] x \lt -\dfrac{1}{2} \\[5ex] Let\:\: x = -1 \\[3ex] 7(-1) + 4 \\[3ex] = -7 + 4 \\[3ex] = -3 $	$ \underline{RHS} \\[3ex] \dfrac{1}{2}(4x + 3) \\[5ex] Must\:\: use\:\: x = -1 \\[3ex] \dfrac{1}{2}(4(-1) + 3)) \\[5ex] = \dfrac{1}{2}(-4 + 3) \\[5ex] = \dfrac{1}{2} * -1 \\[5ex] = -\dfrac{1}{2} $
$-3 \lt -\dfrac{1}{2}$

(6.) WASSCE Given that $Y = \{-2 \le x \le 5\}$ and $W = \{1 \lt x \lt 6\}$, illustrate $Y \cap W$ on the number line.

Assume $Y$ and $W$ contain only integers (even though the question does not specify such)

$ Y = \{-2 \le x \le 5\} \\[3ex] Y = \{-2, -1, 0, 1, 2, 3, 4, 5\} \\[3ex] W = \{2, 3, 4, 5\} \\[3ex] Y \cap W = \{2, 3, 4, 5\} \\[3ex] $ We notice that $Y \cap W$ is the same as $W$
This applies even if they contain other numbers besides integers.
So, $Y \cap W = W$

(7.) ACT When solved for $k$, $-6 + 7k \ge 3 - 8k$ is equivalent to which of the following inequalities?

$ F.\:\: k \ge \dfrac{1}{5} \\[5ex] G.\:\: k \ge \dfrac{3}{5} \\[5ex] H.\:\: k \le \dfrac{5}{3} \\[5ex] J.\:\: k \le 5 \\[3ex] K.\:\: k \ge 9 \\[3ex] $

$ -6 + 7k \ge 3 - 8k \\[3ex] 7k + 8k \ge 3 + 6 \\[3ex] 15k \ge 9 \\[3ex] k \ge \dfrac{9}{15} \\[5ex] k \ge \dfrac{3}{5} \\[5ex] Set\:\:Notation:\:\: \left\{k | k \ge \dfrac{3}{5}\right\} \\[5ex] Interval\:\:Notation:\:\:\left[\dfrac{3}{5}, \infty\right) \\[5ex] $

Check

$ \underline{LHS} \\[3ex] -6 + 7k \\[5ex] k \ge \dfrac{3}{5} \\[5ex] Let\:\: k = 1 \\[3ex] -6 + 7(1) \\[3ex] = -6 + 7 \\[3ex] = 1 $	$ \underline{RHS} \\[3ex] 3 - 8k \\[3ex] Must\:\: use\:\: k = 1 \\[3ex] 3 - 8(1) \\[3ex] = 3 - 8 \\[3ex] = -5 $
$1 \ge -5$

(8.) ACT For real numbers $x$ and $y$ such that $x - y \lt 0$, which of the following must be true?

$ F.\:\: x = y \\[3ex] G.\:\: x \gt y \\[3ex] H.\:\: x \lt y - x \\[3ex] J.\:\: x \lt -y \\[3ex] K.\:\: x \lt y \\[3ex] $

$ x - y \lt 0 \\[3ex] x \lt 0 + y \\[3ex] x \lt y $

(9.) ACT Which of the following is a solution statement for the inequality $3x - 7 \lt 5 + 9x$

$ A.\:\: -2 \lt x \\[3ex] B.\:\: -\dfrac{1}{3} \lt x \\[5ex] C.\:\: -2 \gt x \\[3ex] D.\:\: 1 \gt x \\[3ex] E.\:\: 2 \gt x \\[3ex] $

$ 3x - 7 \lt 5 + 9x \\[3ex] -7 - 5 \lt 9x - 3x \\[3ex] -12 \lt 6x \\[3ex] Swap \\[3ex] Inequality\:\:is\:\:reversed...Note\:\:2 \\[3ex] 6x \gt -12 \\[3ex] x \gt -\dfrac{12}{6} \\[5ex] x \gt -2 \\[3ex] -2 \lt x...for\:\:answer\:\:purposes \\[3ex] Set\:\:Notation:\:\: \{x | x \gt -2\} \\[3ex] Interval\:\:Notation:\:\:(-2, \infty) \\[3ex] $

Check

$ \underline{LHS} \\[3ex] 3x - 7 \\[3ex] x \gt -2 \\[3ex] Let\:\: x = 0 \\[3ex] 3(0) - 7 \\[3ex] = 0 - 7 \\[3ex] = -7 $	$ \underline{RHS} \\[3ex] 5 + 9x \\[3ex] Must\:\: use\:\: x = 0 \\[3ex] 5 + 9(0) \\[3ex] = 5 + 0 \\[3ex] = 5 $
$-7 \lt 5$

(10.) ACT Given real numbers $a, b, c, d$ and $e$ such that $c \lt d$, $e \lt c$, $e \gt b$, and $b \gt a$, which of these numbers is the greatest?

$ A.\:\: a \\[3ex] B.\:\: b \\[3ex] C.\:\: c \\[3ex] D.\:\: d \\[3ex] E.\:\: e \\[3ex] $

We can solve this question in two ways - Numerically and Algebraically
Use any way you prefer.
However, it is better to work with real numbers - solving it Numerically.
So, assign real number values to these variables

$ \underline{First\:\:Method - Numerically} \\[3ex] c \lt d \\[3ex] Let\:\:c = 4,\:\:d = 5 \\[3ex] e \lt c \\[3ex] Let\:\: e = 3\:\:because\:\:3 \lt 4 \\[3ex] e \gt b \\[3ex] Let\:\: b = 2\:\:because\:\:3 \gt 2 \\[3ex] b \gt a \\[3ex] Let\:\: a = 1\:\:because\:\:2 \gt 1 \\[3ex] c = 4,\:\:d = 5,\:\:e = 3,\:\:b = 2,\:\:a = 1 \\[3ex] 5 \gt 4 \gt 3 \gt 2 \gt 1 \\[3ex] d \gt c \gt e \gt b \gt a \\[3ex] \underline{Second\:\:Method - Algebraically} \\[3ex] c \lt d \implies d \gt c \\[3ex] e \lt c \implies c \gt e \\[3ex] e \gt b \\[3ex] b \gt a \\[3ex] \therefore d \gt c \gt e \gt b \gt a \\[3ex] $ The greatest of the numbers is $d$ because $d = 5$

(11.) ACT Which of the following statement for the inequality $6x - 6 \lt 7 + 10x$?

$ F.\:\: -\dfrac{13}{4} \lt x \\[5ex] G.\:\: -\dfrac{1}{4} \lt x \\[5ex] H.\:\: -\dfrac{13}{4} \gt x \\[5ex] J.\:\: \dfrac{13}{16} \gt x \\[5ex] K.\:\: \dfrac{13}{4} \gt x \\[5ex] $

$ 6x - 6 \lt 7 + 10x \\[3ex] 6x - 10x \lt 7 + 6 \\[3ex] -4x \lt 13 \\[3ex] Divide\:\:both\:\:sides\:\:by\:\:-4 \\[3ex] Inequality\:\:is\:\:reversed...Note\:\:1 \\[3ex] x \gt -\dfrac{13}{4} \\[5ex] -\dfrac{13}{4} \lt x...for\:\:answer\:\:purposes \\[5ex] Set\:\:Notation:\:\: \left\{x | x \gt -\dfrac{13}{4}\right\} \\[5ex] Interval\:\:Notation:\:\:\left(-\dfrac{13}{4}, \infty\right) \\[5ex] $

Check

$ \underline{LHS} \\[3ex] 6x - 6 \\[3ex] x \gt -\dfrac{13}{4} \\[5ex] Let\:\: x = 1 \\[3ex] 6(1) - 6 \\[3ex] = 6 - 6 \\[3ex] = 0 $	$ \underline{RHS} \\[3ex] 7 + 10x \\[3ex] Must\:\: use\:\: x = 1 \\[3ex] 7 + 10(1) \\[3ex] = 7 + 10 \\[3ex] = 17 $
$0 \lt 17$

(12.) ACT When $a$, $b$, and $c$ are real numbers and $ab^2c^4 \gt 0$, which of the following must be greater than $0$?

$ F.\:\: ac^2 \\[3ex] G.\:\: ac \\[3ex] H.\:\: ab \\[3ex] J.\:\: abc \\[3ex] K.\:\: bc \\[3ex] $

$ ab^2c^4 \gt 0 \\[3ex] \gt 0\:\:means\:\:a\:\:positive\:\:number \\[3ex] b^2\:\:must\:\:be\:\:positive \\[3ex] $ Why?
This is because the square of any non-zero number is positive

$ Let\:\:b = -3 \\[3ex] b^2 = (-3)^2 = 9 \\[3ex] Let\:\:b = 3 \\[3ex] b^2 = (3)^2 = 9 \\[3ex] Also \\[3ex] c^4\:\:must\:\:be\:\:positive \\[3ex] $ Why?
This is because any non-zero number(base) raised to an even exponent gives a positive result

$ Let\:\:c = -2 \\[3ex] c^4 = (-2)^4 = (-2)(-2)(-2)(-2) = 16 \\[3ex] Let\:\:c = 2 \\[3ex] c^4 = (2)^4 = (2)(2)(2)(2) = 16 \\[3ex] $ If $b^2$ is positive and $c^4$ is positive, then $a$ must be positive

Why? This is because the the product of positives must give a positive result.
If $a$ was not positive, then the product will not be greater than $0$
If $a$ was negative, then the product will be less than $0$
But, the product on the LHS (Left Hand Side) is positive (greater than $0$)
So, $a$ must be positive
$a$ is greater than $0$

Let us analyze the options

$ F.\:\: ac^2 \\[3ex] a\:\:is\:\:positive \\[3ex] c^2\:\:is\:\:positive \\[3ex] positive * positive = positive \\[3ex] \therefore ac^2\:\:is\:\:positive \\[3ex] ac^2 \gt 0 \\[3ex] Option\:\:F\:\:is\:\:correct \\[3ex] G.\:\: ac \\[3ex] a\:\:is\:\:positive \\[3ex] But\:\:c\:\:could\:\:be\:\:negative \\[3ex] When\:\:c\:\:is\:\:negative \\[3ex] positive * negative = negative \\[3ex] ac\:\:is\:\:negative \\[3ex] ac \lt 0 \\[3ex] Option\:\:G\:\:is\:\:incorrect \\[3ex] H.\:\: ab \\[3ex] a\:\:is\:\:positive \\[3ex] But\:\:b\:\:could\:\:be\:\:negative \\[3ex] When\:\:b\:\:is\:\:negative \\[3ex] positive * negative = negative \\[3ex] ab\:\:is\:\:negative \\[3ex] ab \lt 0 \\[3ex] Option\:\:H\:\:is\:\:incorrect \\[3ex] J.\:\: abc \\[3ex] a\:\:is\:\:positive \\[3ex] But\:\:b\:\:could\:\:be\:\:negative \\[3ex] And\:\:c\:\:could\:\:be\:\:positive \\[3ex] When\:\:b\:\:is\:\:negative\:\:and\:\:c\:\:is\:\:positive \\[3ex] positive * negative * positive = negative \\[3ex] abc\:\:is\:\:negative \\[3ex] abc \lt 0 \\[3ex] Option\:\:J\:\:is\:\:incorrect \\[3ex] K.\:\: bc \\[3ex] b\:\:could\:\:be\:\:positive \\[3ex] And\:\:c\:\:could\:\:be\:\:negative \\[3ex] When\:\:b\:\:is\:\:positive\:\:and\:\:c\:\:is\:\:negative \\[3ex] positive * negative = negative \\[3ex] bc\:\:is\:\:negative \\[3ex] bc \lt 0 \\[3ex] Option\:\:K\:\:is\:\:incorrect $

(14.) CSEC (a) (i) Solve for x, where x is a real number.
$8 - x \le 5x + 2$

(ii) Show your solution to (a)(i) on the number line.

$ 8 - x \le 5x + 2 \\[3ex] Swap \\[3ex] Inequality\:\:is\:\:reversed...Note\:\:2 \\[3ex] 5x + 2 \ge 8 - x \\[3ex] $ Student: May I ask - why did you swap?
Teacher: I do not want to divide by a negative number
Student: Okay, you did not want to divide both sides by $-6$?
Teacher: That is correct!
Student: But, what if I decide not to swap and divide both sides by $-6$?
Teacher: That would still be a correct method.
We did the same method in Question $11$

$ 5x + 2 \ge 8 - x \\[3ex] 5x + x \ge 8 - 2 \\[3ex] 6x \ge 6 \\[3ex] x \ge \dfrac{6}{6} \\[5ex] x \ge 1 \\[3ex] Set\:\:Notation:\:\: \{x | x \ge 1\} \\[3ex] Interval\:\:Notation:\:\:[1, \infty) \\[3ex] $

Check

$ \{x | x \ge 1\} $
LHS	RHS
$ 8 - x \\[3ex] x \ge 1 \\[3ex] Let\:\: x = 3 \\[3ex] 8 - 3 \\[3ex] = 5 $	$ 5x + 2 \\[3ex] Must\:\: use\:\: x = 3 \\[3ex] 5(3) + 2 \\[3ex] = 15 + 2 \\[3ex] = 17 $
$5 \le 17$

(15.) WASSCE $7(x + 4) - \dfrac{2}{3}(x - 6) \le 2[x - 3(x + 5)]$

$ 7(x + 4) - \dfrac{2}{3}(x - 6) \le 2[x - 3(x + 5)] \\[5ex] $ Do you like fractions? ☺

Let us clear the fractions

$LCD = 3$
Multiply each term by the $LCD$

$ 3 * 7(x + 4) - 3 * \dfrac{2}{3}(x - 6) \le 3 * 2[x - 3(x + 5)] \\[5ex] 21(x + 4) - 2(x - 6) \le 6[x - 3(x + 5)] \\[3ex] 21x + 84 - 2x + 12 \le 6[x - 3x - 15] \\[3ex] 19x + 96 \le 6(-2x - 15) \\[3ex] 19x + 96 \le -12x - 90 \\[3ex] 19x + 12x \le -90 - 96 \\[3ex] 31x \le -186 \\[3ex] x \le -\dfrac{186}{31} \\[5ex] x \le - 6 \\[3ex] Set\:\:Notation:\:\: \{x | x \le -6\} \\[5ex] Interval\:\:Notation:\:\:(-\infty, -6] \\[3ex] $

Check

$ \{x | x \le -6\} $
LHS	RHS
$ 7(x + 4) - \dfrac{2}{3}(x - 6) \\[5ex] x \le -6 \\[3ex] Let\:\: x = -9 \\[3ex] $ Student: Why did you choose $-9$ Teacher: Because I want a number that is divisible by $3$ $-9 - 6 = -15$ $-15$ is divisible by $3$ Student: Could you not have chosen $-6$? Because $-6 \le -6$ Teacher: I could have. However, I do not want to check my solution as an equation. $ 7(-9 + 4) - \dfrac{2}{3}(-9 - 6) \\[5ex] = 7(-5) - \dfrac{2}{3}(-15) \\[5ex] = -35 - 2(-5) \\[3ex] = -35 + 10 \\[3ex] = -25 $	$ 2[x - 3(x + 5)] \\[3ex] Must\:\: use\:\: x = -9 \\[3ex] = 2[-9 - 3(-9 + 5)] \\[3ex] = 2[-9 - 3(-4)] \\[3ex] = 2[-9 + 12] \\[3ex] = 2(3) \\[3ex] = 6 $
$-25 \le 6$

(16.) CSEC Solve for x

(i) $2x - 7 \le 3$

(ii) If x is a positive integer, list the possible values of x

$ (i) \\[3ex] 2x - 7 \le 3 \\[3ex] 2x \le 3 + 7 \\[3ex] 2x \le 10 \\[3ex] x \le \dfrac{10}{2} \\[5ex] x \le 5 \\[3ex] Set\:\:Notation:\:\: \{x | x \le 5\} \\[3ex] Interval\:\:Notation:\:\:(-\infty, 5] \\[3ex] (ii) \\[3ex] All\:\:the\:\:positive\:\:integer\:\:values\:\:of\:\:x = 1, 2, 3, 4, 5 \\[3ex] $ NOTE: 0 is not a positive integer.
0 is a nonpositive integer.
0 is also a nonnegative integer.

Ask students to explain the difference between a positive integer and a nonpositive integer
Ask them to explain the difference between a positive integer and a nonpositive integer
They should give examples in both cases.

$

Check

$ \{x | x \le 5\}
Let\;\;x = 0 $
LHS	RHS
$ 2x - 7 \\[5ex] 2(0) - 7 \\[3ex] 0 - 7 \\[3ex] -7 $	$3$
$-7 \le 3$